WOI-LevSearch
The fuzzy search using the Levenshtein distance
Filemaker Add-On WOI-LevSearch
The fuzzy search using the Levenshtein distance
The Levenshtein distance between two strings is the minimum number of insertion, deletion, and substitution operations required to transform the first string into the second. The distance is named after the Russian scientist Vladimir Levenshtein, who introduced it in 1965.
We can see from the result that the name “Qoute” in connection with the first name “Emil” does not match the searched name “Woide.”
The Levenshtein algorithm is used in Google search and, for example, also in WORD for error correction.
First, a simple example with the name “Miller”, which clearly shows how it works.
If you enter exactly this sequence of letters in the search field of a database, you will find the correct data record. However, you will not find the data record you are looking for if it is saved under the misspelled name “Killer”.
If we now apply the Levenshtein distance, the value is “1”, since exactly one operation is necessary to turn “Miller” into “Killer”, namely replacing the letter “M” with “K”.
For the fuzzy search, this means that the Levenshtein distance is determined for the search field in each data record.
A second example illustrates how the behavior of the search result changes when the default Levenshtein distance is increased. Let’s stick with the example “Miller” and specify the Levenshtein distance with the value “3”.
This means that we find all names that can be created with exactly 3 operations, such as “Mother.” This add-on implements the algorithm in such a way that it can be used for any existing
FileMaker solution without the need for programming.
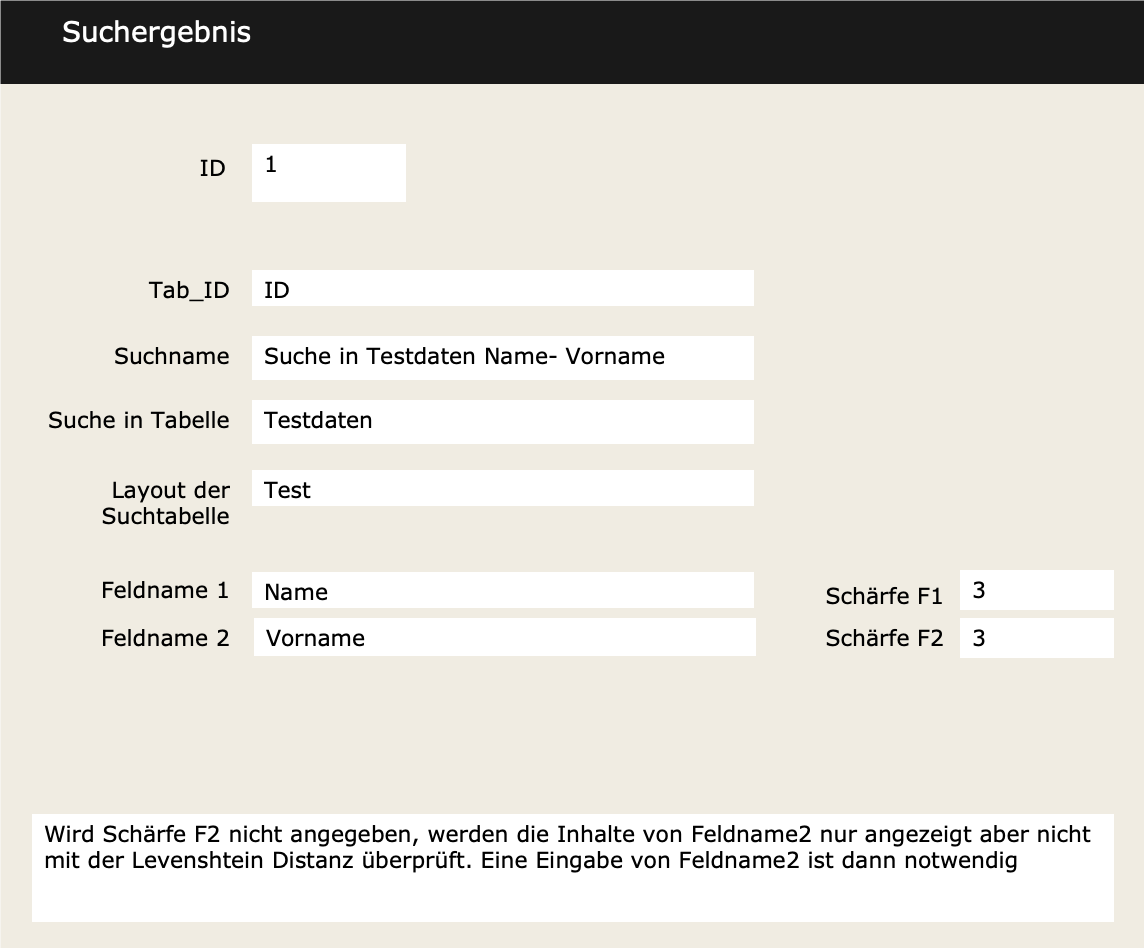
In addition, the possibility was created to activate the algorithm in a second field.
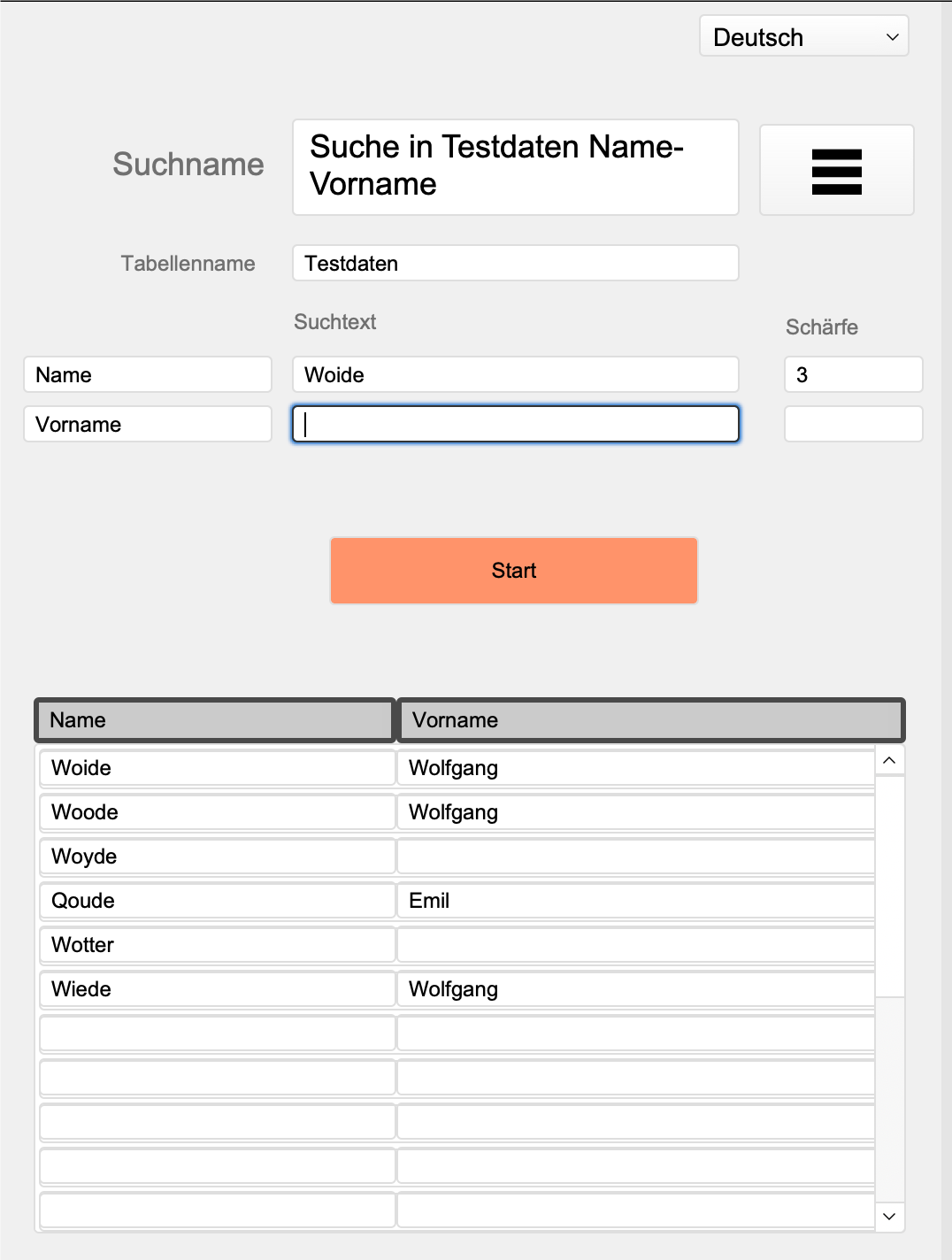
If you now specify the sharpness for the Levenshtein distance with “3”, the result looks like this:
The results are not automatically true or false. In our example, we see that with “Woyde” the first name is missing, but the spelling can be either true or false, because the name “Woyde” really exists.
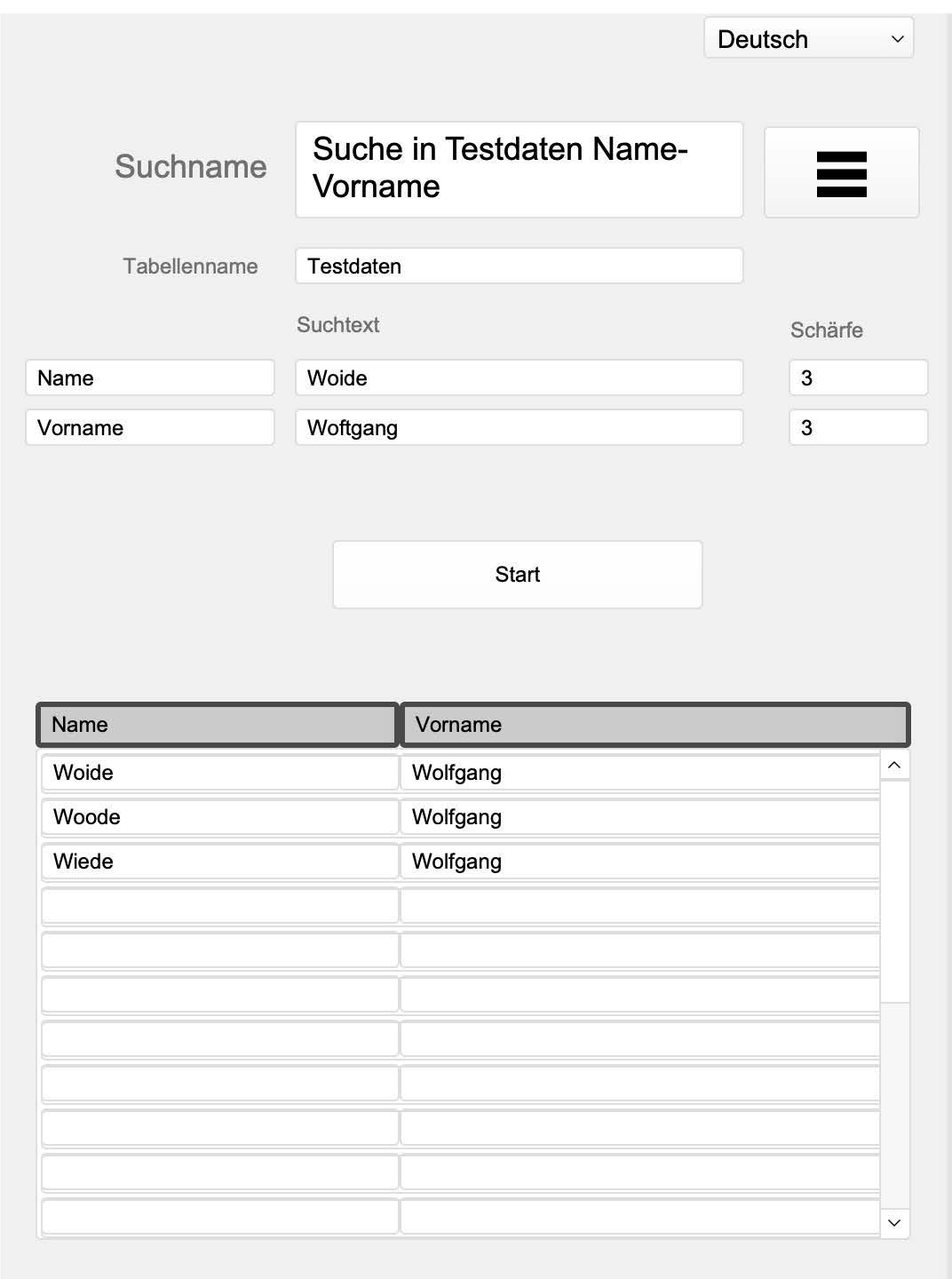
For this reason, I decided to apply the Levenshtein distance to the second field as well. So we get this result:
There is an extension of Levenshtein’s algorithm that also recognizes transposed letters. A transposition is rated with only one operation, while the original algorithm requires 2 operations.
This algorithm is called Levenshtein-Damerau. This extension is quite helpful in practice, as input transpositions are relatively common and difficult to find.
To make these results available in an add-on for any table, a parameter table is added upstream, in which the necessary information can be entered.
